Вычисление расстояния между двумя произвольными линиями по любой прямой — это задача, которая может быть полезной в различных областях, таких как геометрия, картография или компьютерная графика. Для решения этой задачи можно использовать различные методы, включая геометрические алгоритмы или математические формулы. В данной статье мы рассмотрим несколько методов вычисления расстояния между двумя линиями по прямой и представим примеры их использования.
Определение исходных данных
Для вычисления расстояния между двумя произвольными линиями по любой прямой необходимо иметь следующие исходные данные:
- Координаты точек на каждой из линий
- Угол наклона каждой из линий (если применяется не горизонтальная или вертикальная прямая)
Координаты точек делятся на две группы: точки первой линии (A, B) и точки второй линии (C, D). Каждая точка указывается своими координатами X и Y.
Угол наклона линии обычно измеряется в градусах и указывает направление линии относительно горизонтальной оси. Вертикальные и горизонтальные линии имеют нулевой угол наклона.

Пример:
- Точка A: X = 2, Y = 3
- Точка B: X = 5, Y = 8
- Точка C: X = 1, Y = 1
- Точка D: X = 6, Y = 6
- Угол наклона первой линии: 45 градусов
- Угол наклона второй линии: 30 градусов
Исходные данные определяют геометрическую конфигурацию линий, которая позволяет вычислить расстояние между ними. Также важно учесть единицы измерения координат и углов, например, метры и градусы.
Построение прямой
Методы построения
В зависимости от имеющихся данных, существуют различные методы построения прямой:
- Построение по двум точкам: для этого метода необходимо знать координаты двух точек на прямой. Сначала проводится прямая через эти две точки, а затем можно продлить ее в обе стороны при необходимости.
- Построение по точке и направлению: при данном подходе известны координаты одной точки и вектор направления прямой. Сначала проводится линия через заданную точку параллельно данному вектору.
- Построение параллельной прямой: при данном методе известны координаты одной точки на первой прямой и расстояние между этой точкой и новой параллельной прямой. Сначала проводится перпендикуляр в заданной точке к первой прямой, а затем заданное расстояние при помощи параллельной линии.
- Построение перпендикулярной прямой: для этого метода необходимо знать координаты точки на первой прямой и угол между первой прямой и перпендикулярной прямой. Сначала проводится линия через заданную точку под нужным углом к первой прямой.
Примеры построения прямых
Для демонстрации построения прямых рассмотрим несколько практических примеров:
- Построение прямой через точки A(2, 3) и B(5, 7).
- Построение прямой через точку C(4, 1) с направлением (2, 3).
- Построение прямой, параллельной прямой AB, через точку D(6, 4).
- Построение прямой, перпендикулярной прямой AB, через точку E(8, 2) с углом 60 градусов.
Используя соответствующие методы для каждого примера, можно точно построить требуемые прямые.
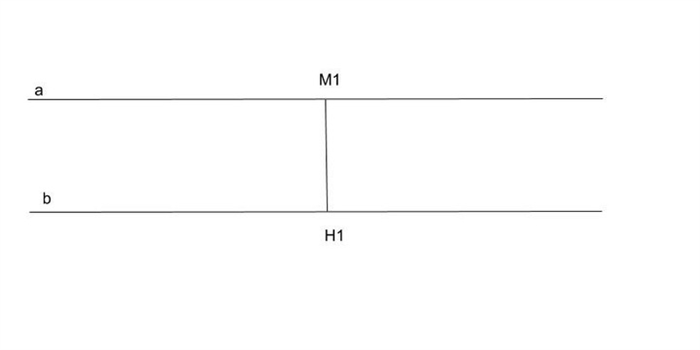
Поиск пересечений с линиями
При решении задач по вычислению расстояния между двумя произвольными линиями по любой прямой возникает необходимость найти точки их пересечения. В данном материале рассмотрим подходы к поиску пересечений линий, которые могут быть использованы в таких задачах.
Метод графического поиска пересечений
Один из способов поиска пересечений линий — графический метод, который основан на построении графика каждой из линий и анализе их взаимного расположения. Для этого необходимо:
- Задать уравнения прямых, задающих линии
- Построить графики линий на координатной плоскости
- Определить точки пересечения линий, если они существуют
Полученные точки пересечения могут быть использованы для дальнейшего вычисления расстояния между линиями по выбранной прямой.
Метод аналитического поиска пересечений
Альтернативным подходом является аналитический метод поиска пересечений линий, который основан на анализе уравнений линий и системы уравнений. Для его применения необходимо:
- Задать уравнения прямых, задающих линии
- Решить систему уравнений, составленную из уравнений линий
- Определить точки пересечения линий, если они существуют
Таким образом, аналитический метод позволяет найти точки пересечения линий через анализ их уравнений, что может быть полезно при решении задач по вычислению расстояния между линиями.
Особенности поиска пересечений
При поиске пересечений линий необходимо учитывать, что:

- Пересечения линий могут быть как единственными, так и множественными, в зависимости от их взаимного расположения
- В случае, если линии параллельны или совпадают, пересечений не существует
- В ряде задач может потребоваться определение точек пересечения множества линий, а не только двух
Учитывая эти особенности, методы поиска пересечений линий могут быть применены для решения задач по вычислению расстояния между линиями по любой прямой с учетом их геометрического расположения.
Определение расстояния между пересечениями
Для определения расстояния между пересечениями можно использовать несколько методов, включая геометрический анализ и алгебраические формулы.
Геометрический анализ
При использовании геометрического анализа для определения расстояния между пересечениями, необходимо выполнить следующие шаги:
- Изобразите две линии на координатной плоскости.
- Определите точки их пересечения.
- Проведите прямую, проходящую через эти точки.
- Измерьте расстояние между пересечениями по заданной прямой.
Геометрический анализ позволяет наглядно представить расположение линий и точек пересечения, что облегчает определение расстояния между пересечениями.
Алгебраические формулы
Алгебраический подход к определению расстояния между пересечениями основан на использовании уравнений прямых. Для вычисления расстояния между пересечениями необходимо выполнить следующие действия:
- Запишите уравнения двух линий.
- Решите систему уравнений для определения точек пересечения.
- Вычислите расстояние между пересечениями по определенным точкам, используя соответствующую формулу.
Алгебраический подход обеспечивает точное вычисление расстояния между пересечениями, позволяя получить численное значение без необходимости проведения графических построений.
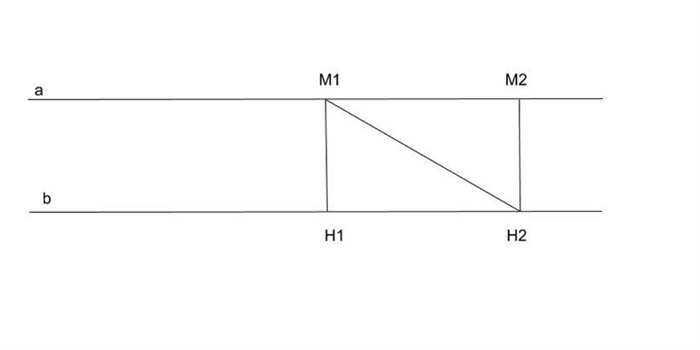
Применение в практике
Определение расстояния между пересечениями применяется в различных областях, включая геодезию, инженерию, архитектуру и компьютерную графику. Например, при проектировании дорожных сетей необходимо определить расстояние между перекрестками, чтобы обеспечить безопасную и эффективную организацию движения.
Расчет расстояния по прямой
При необходимости вычисления расстояния между двумя произвольными линиями по любой прямой следует учитывать несколько важных факторов.
1. Определение точек на линиях
Первым шагом в расчете расстояния по прямой является определение точек на каждой из линий. Для этого необходимо взять произвольную точку на одной линии, а затем провести перпендикуляр к другой линии. Точка пересечения перпендикуляра с линией будет являться второй точкой.
2. Вычисление расстояния между точками
После определения двух точек на линиях можно приступить к вычислению расстояния между ними. Для этого используется формула расстояния между двумя точками в пространстве. Формула выглядит следующим образом:
Расстояние = √((x2 — x1)² + (y2 — y1)² + (z2 — z1)²).
Здесь (x1, y1, z1) и (x2, y2, z2) — координаты первой и второй точек соответственно.
3. Использование прямой, соединяющей точки
После вычисления расстояния между точками можно использовать прямую, соединяющую эти точки, для расчета расстояния по любой другой прямой. Для этого необходимо задать направляющий вектор этой прямой и вычислить расстояние от произвольной точки на этой прямой до линий.
4. Определение пересекающихся точек
Для расчета расстояния по другой прямой необходимо определить точки, в которых эта прямая пересекает каждую из линий. Для этого решается система уравнений, состоящая из уравнений прямых и уравнения прямой, заданной направляющим вектором и произвольной точкой.
5. Вычисление расстояния
После определения пересекающихся точек можно приступить к расчету самого расстояния. Для этого необходимо вычислить длину отрезка между точками пересечения прямой и линий. Данное расстояние будет являться искомым расстоянием между двумя произвольными линиями по заданной прямой.
Проверка результатов
После проведения расчётов для определения расстояния между двумя произвольными линиями по любой прямой, необходимо выполнить проверку полученных результатов. В этом случае, следует применить несколько методов, чтобы убедиться в достоверности полученных данных.
1. Сравнение с известными значениями
2. Построение графиков
3. Дополнительные методы проверки
Кроме сравнения с известными значениями и построения графиков, существуют и другие дополнительные методы проверки результатов. Например, можно провести повторные расчёты с использованием других моделей или методов для сравнения результатов. Также возможно проведение аналитической проверки, путём анализа полученных формул и вычислений.
Важно отметить, что проверка результатов является неотъемлемой частью процесса вычисления расстояния между двумя произвольными линиями по любой прямой. Она помогает убедиться в правильности расчетов и повысить достоверность полученных данных. При обнаружении расхождений следует провести дополнительные исследования или проверки для выявления возможных ошибок или неточностей.
Визуализация решения
1. Разделение линий на отрезки
Первый шаг визуализации решения заключается в разделении обеих линий на отрезки. Это позволяет более точно определить места пересечения и расстояние между ними. Для этого необходимо:
- Выбрать две линии, между которыми необходимо вычислить расстояние.
- Разделить каждую из линий на отрезки заданной длины. Рекомендуется выбрать длину отрезков таким образом, чтобы визуализировать все существенные точки на линии.
2. Поиск пересечений
Второй шаг заключается в поиске точек пересечения между отрезками двух линий. Это позволяет найти точки, между которыми необходимо вычислить расстояние. Для этого необходимо:
- Сравнить каждый отрезок одной линии с каждым отрезком другой линии и найти точки пересечения.
- Записать координаты этих точек для дальнейшего вычисления расстояния.
3. Вычисление расстояния
Третий шаг заключается в вычислении расстояния между точками пересечения на основе выбранной прямой. Для этого необходимо:
- Выбрать прямую, относительно которой будет измерено расстояние (например, горизонтальную или вертикальную).
- Измерить расстояние между выбранной прямой и каждой точкой пересечения с помощью формулы нахождения расстояния между двумя точками.
- Записать полученные значения расстояний.
Пример визуализации решения
| Линия A | Линия B |
|---|---|
| Отрезок 1 | Отрезок 1 |
| Отрезок 2 | Отрезок 2 |
| Точка пересечения 1 | Точка пересечения 1 |
| Точка пересечения 2 | Точка пересечения 2 |
| Расстояние от отрезка 1 до прямой | Расстояние от отрезка 1 до прямой |
| Расстояние от отрезка 2 до прямой | Расстояние от отрезка 2 до прямой |
Таким образом, визуализация решения позволяет наглядно представить расстояние между двумя произвольными линиями по любой прямой. Этот подход особенно полезен при решении задач, связанных с геометрическими конструкциями и нахождением оптимальных путей.
Практическое применение
Метод вычисления расстояния между двумя произвольными линиями по любой прямой имеет множество практических применений в различных областях. Ниже представлены некоторые практические сферы применения данного метода:
- Геодезия и инженерия: Определение расстояния между двумя линиями может быть полезно при планировании и строительстве различных инженерных сооружений, таких как дороги, мосты и здания. Этот метод позволяет точно вычислить расстояние между двумя объектами на местности, что позволяет инженерам и геодезистам оптимизировать проектирование и строительство.
- Картография и география: Вычисление расстояния между линиями на карте позволяет определять расстояние между географическими объектами, такими как города, озера и реки. Это важно при планировании маршрутов, изучении территории и анализе географических данных.
- Физика и математика: Данный метод находит применение в физике и математике при решении различных задач. Например, при моделировании движения тел в пространстве или при вычислении оптических путей лучей света.
- Компьютерная графика и визуализация: Расчет расстояния между линиями может быть полезным при создании компьютерных моделей и визуализации трехмерных объектов. Этот метод позволяет точно определить расстояние между двумя объектами и использовать эту информацию при создании реалистичных и эффективных графических сцен.
В общем, метод вычисления расстояния между двумя произвольными линиями по любой прямой имеет широкое практическое применение во многих областях, включая геодезию, инженерию, картографию, физику, математику, компьютерную графику и визуализацию. Этот метод позволяет определить точное расстояние между объектами и использовать эту информацию для различных целей, таких как планирование, моделирование и анализ данных.